Historically, Analytical Ultracentrifugation was readily applied for the determination of diffusion coefficients. Since then, dynamic light scattering has dominated. Today, Analytical Ultracentrifugation plays a minor part, but it can contribute valuable services in special cases.
Such cases may be
- when polydispersities, corrected for diffusion, are to be determined,
- when diffusion constants of particles are to be determined in motion,
- when particles are too small to be characterized via dynamic light scattering,
- when multimodal mixtures are to be examined,
- …
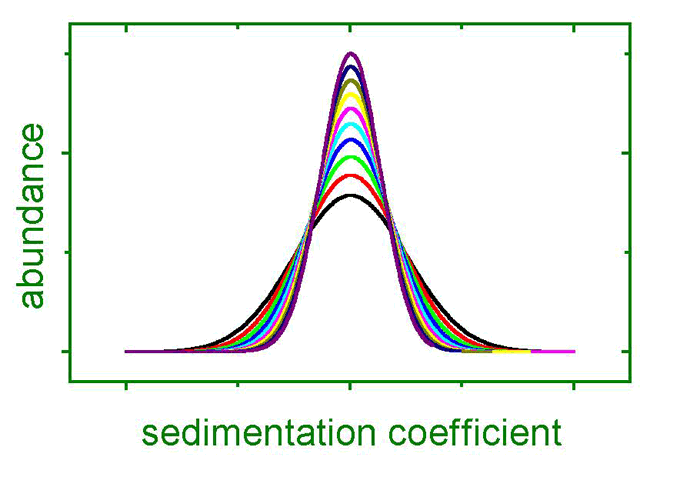
When discussing Analytical Ultracentrifugation, the transport process of sedimentation is naturally in the focus. It is often overlooked than another transport process is inherent: diffusion along the concentration gradients induced by sedimentation. Both processes are accounted for by the Lamm equation, published in 1921. However, during most of the 20th century, it was not possible to perform global fitting to solutions of this (differential) equation – the strategy was rather to separate both processes, either by conducting sedimentation velocity experiments at high angular velocities and short experimental durations (suppressing diffusion effects) or at low angular velocities and long durations (retarding sedimentation).
Modern computers allow for global fitting of both processes, and many software solutions have been developed since. However, the classical approaches, focussing on either of the processes and utilizing specific evaluation algorithms, are still in practise. Most prominent is the synthetic boundary experiment, where a special measurement cell is used: The analyte of interest is brought onto the surface of the solvent at low angular velocities, forming a boundary that will spread into the solvent by diffusion. This process is monitored, allowing to calculate the diffusion coefficient. Gravitational forces are kept as low as possible as it is not intended to sediment the particles.
However, diffusion processes can also be analyzed on moving boundaries, as in a classical sedimentation velocity experiment. Here, particles will diffuse along the concentration decrease at the sedimentation boundary. This phenomenon causes the sedimentation boundary to broaden with increasing time. When transforming the concentration profiles into sedimentation coefficients, as shown in the figure, it becomes apparent that the broadness of the transformed boundaries changes with time. Paradoxically, the broadest peaks resemble the beginning of the experiment, getting narrower as sedimentation progresses. This is due to the fact that sedimentation is proportional to time whereas diffusion is proportional to the square root of time.
There are classical and modern approaches for separating diffusion and sedimentation. For instance, we have developed an approach for separating the contributions of polydispersity and diffusion to boundary spreading. From this, as well the “real” polydispersity as the diffusion coefficient are obtained.
In principle, classical approaches have intended to suppress or enhance either process experimentally and applying evaluation procedures focussing on the process of interest. It was recognized that either other process would obscure or overlay the evaluation of the target property. With modern computing, diffusion has mutated from an obstacle to a source of information, comprised in global fitting of both simultaneous transport processes.
Further theoretical background can be found on our scientific website under www.analytical-ultracentrifugation.com.

