The sedimentation velocity experiment is the most popular among all Analytical Ultracentrifugation techniques. The data obtained can be evaluated in various ways, yielding a large scope of results. Without any assumptions, the sedimentation coeffifient distribution (in short: s-distribution) is obtained, giving fundamental information:
- How many components are contained?
- Are these components poly- or monodisperse?
- Do the components sediment rather quickly or slowly?
Introducing assumptions and models, further results are derived from the s-distribution, such as
- particle size distributions
- particle density distributions
- molar mass distributions
- diffusion coefficients
The s-distribution is independent on the individual nature of the particle. It simply gives a measure for how rapidly a particle or molecule will sediment in a given field of gravity. No assumptions are carried into ist calculation. The s-distribution is the primary result of measurement.
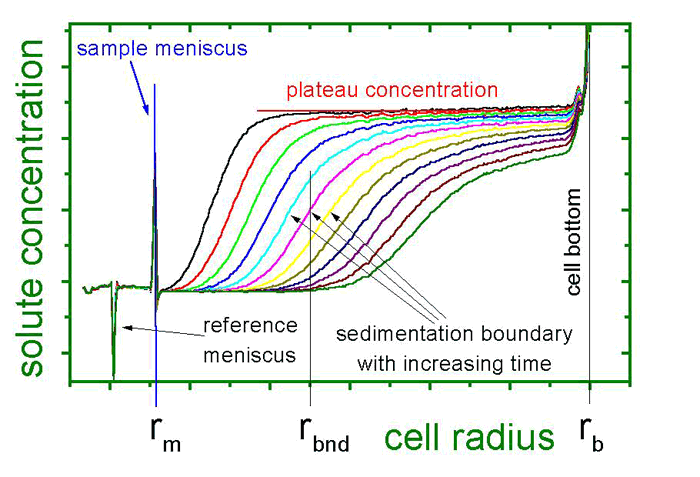
A sedimentation velocity run is rather fast, making it the cheapest among all Analytical Ultracentrifugation experiments. In the neighboring figure, consecutive scans of a sedimentation velocity experiment are displayed. They show the sedimentation profiles of a sedimenting species at constant time intervals.
The sedimentation constant of a particle with given molar mass, density, and shape is also dependent on temperature, pressure, solvent density, and solvent viscosity. Thus, the experiment is either conducted under standard conditions, or the constant is corrected for these conditions.
By means of further calculation, the s-distribution can be converted into particle size and molecular mass distributions. Density distributions and diffusion constants are also available from this primary result. Specifically:
- Particle size distributions can be obtained by direct calculation with known particle density.
- With unknown particle density, a density distribution is obtained by comparing s-distributions from two sedimentation velocity experiments performed in solvents of different density. This procedure is called density variation.
- Molar mass distributions are obtained by including particle density and frictional properties.
- Diffusion coefficients are calculated from the time-dependent broadening of the sedimentation boundary.
With modern computing algorithms, comprehensive modelling of particles and macromolecules, including their frictional properties, can be achieved by global fitting to solutions of the Lamm equation, accounting for both sedimentation and diffusion processes.

