- Analytische Ultrazentrifugation (AUZ)
- Prinzip der AUZ
- Die AUZ – eine vielseitige Meßmethode
- Mittels AUZ zugängliche Eigenschaften
- Kombination mit anderen Methoden
- Historische Methode, moderne Trends
- AUZ als Auftragsmessung
1. Analytische Ultrazentrifugation (AUZ)
Mächtiges Werkzeug der Kolloid- und Polymeranalytik
Seit mehr als 90 Jahren leistet die Analytische Ultrazentrifugation (AUZ) unschätzbare Dienste in der Biochemie und in den Kolloidwissenschaften. Das Anwendungsfeld der AUZ in Chemie, Biochemie und Pharmazie ist breit gestreut: die Methode gestattet u. a. die Bestimmung von Molmassen, Molmassenverteilungen, Teilchengrößenverteilungen und Teilchendichteverteilungen.
Untersucht werden können Partikel, Knäuel, Mizellen – letztlich alle dispergierten oder gelösten Teilchen beliebiger Art, die im Schwerefeld sedimentieren oder flotieren.

Bei einer maximalen Drehzahl von 60000 U/min entwickelt die Analytische Ultrazentrifuge ein Schwerefeld, das dem 260000fachen der Erdbeschleunigung entspricht. Unter dem Einfluss dieses Feldes werden nahezu beliebige Partikel zum Sedimentieren oder Flotieren gezwungen. Dieser Vorgang wird optisch detektiert und interpretiert.
Handelsübliche AUZ sind mit Absorptions- oder Interferenzdetektoren ausgestattet. Darüber hinaus gibt es Fluoreszenzdetektoren und Multiwellenlängen-Absorptionsdetektoren; in der Entwicklung befinden sich außerdem Raman-, Trübungs- und Streudetektoren. Die traditionelle Schlierenoptik ist nicht mehr verfügbar.
2. Prinzip der AUZ
Die Analytische Ultrazentrifugation besticht durch die Anschaulichkeit ihres Meßprinzips: So wie eine große Kugel im Wasser schneller zu Boden sinkt als eine kleinere, eine Stahlkugel schneller als eine ebenso große aus Aluminium, eine Kugel schneller als ein Stäbchen oder Knäuel gleicher Masse, so fraktioniert die AUZ nach Teilchengröße, Teilchendichte und Form.

Während der Sedimentation wird die Meßzelle parallel zur Rotationsachse von optischen Systemen durchstrahlt. Die Abbildung zeigt eine klassische Absorptionsoptik. Man erhält ein ortsaufgelöstes Konzentrationsprofil über den radialen Verlauf der Meßzelle; diese Messung wird während des Experiments wiederholt, wodurch zusätzlich eine zeitaufgelöste Information erhalten wird.
Unterschiedliche Komponenten fraktionieren im Verlauf der Sedimentation. Die Konzentrationsprofile werden hinsichtlich der gewünschten Information ausgewertet.
Das Bild zeigt ortsaufgelöste Konzentrationsprofile innerhalb der Meßzelle, wie sie von den optischen Systemen der AUZ detektiert werden. Vom Meniskus her verarmt die Lösung an Partikeln; am Zellboden reichern sie sich an. An der sogenannten Sedimentationsfront steigt die Konzentration an Partikeln stark an.
Im zeitlichen Verlauf der Sedimentation wandert die Sedimentationsfront zum Zellboden; aus der Geschwindigkeit dieser Wanderung sind Partikeleigenschaften zugänglich. Bei Anwesenheit mehrerer Partikelsorten werden ebenso viele Sedimentationsfronten beobachtet.
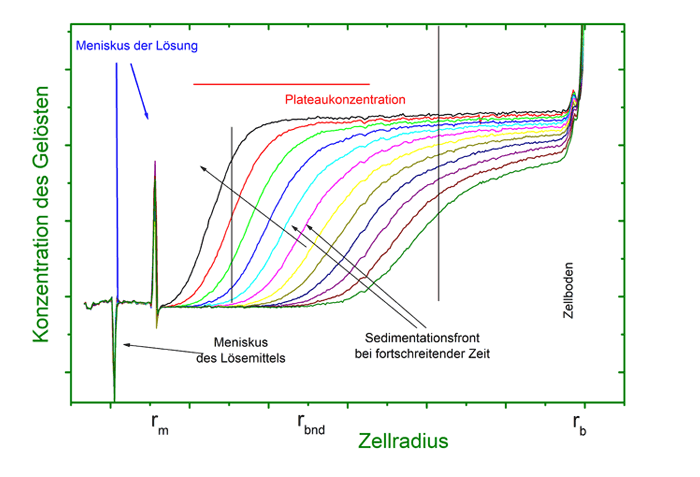
Außer der Sedimentation sind die Teilchen auch der Diffusion ausgesetzt. Mit der Anreicherung des Materials am Zellboden wird diese Rückdiffusion stärker, so dass sich am Ende des Experiments ein Gleichgewicht zwischen Sedimentation und Diffusion ausbildet. Dieses sogenannte Sedimentations-Diffusions-Gleichgewicht bietet eigene Auswertungsmöglichkeiten, da hier keine Transportprozesse mehr stattfinden. Oft werden jedoch schon aus dem Verlauf des Sedimentationsprozesses die gewünschten Informationen erhalten.
3. Die AUZ – eine vielseitige Meßmethode
Die AUZ ist eine Absolutmethode und erfordert keine Kalibrierung. Es treten keine Wechselwirkungen mit einer stationären Phase auf. Nahezu beliebige Lösemittel sind einsetzbar. Die benötigten Probenmengen sind sehr klein, was den Einsatz insbesondere in der Biochemie attraktiv macht. Auch das Lösemittel wird nur in kleinen Mengen benötigt.
Allein eine Aufzählung der Basisexperimente verdeutlicht die vielseitige Einsetzbarkeit der AUZ:
- Sedimentationsgeschwindigkeitsexperiment
- Sedimentationsgleichgewichtsexperiment
- Dichtegradient
- Überschichtungsexperiment
Dazu existieren Varianten zu allen Basisexperimenten, die je nach Fragestellung zum Einsatz kommen.
Ebenso vielseitig wie die experimentellen Techniken sind die Zielsysteme: Zugänglich sind Partikel bzw. Moleküle von wenigen Nanometern bis mehreren Mikrometern im Durchmesser, entsprechend Molmassen von wenigen Tausend bis etlichen Millionen g/mol. Auch organische Lösemittel, saure oder basische Systeme sowie hochviskose Proben stellen kein prinzipielles Problem dar. Optimal sind hierfür Zellenkörper aus Titan; marktüblich sind Kunststoff- und Aluminiumzellen, die für die meisten wässrigen Anwendungen ausreichen. Die Küvettenfenster bestehen aus Quarz oder Saphir.
Entscheidend für den erfolgreichen Einsatz der AUZ sind die Detektoren. Insbesondere die Kombination einer (spezifischen) Absorptionsoptik mit einer (unspezifischen) Interferenzoptik macht nicht nur eine Vielzahl von Systemen zugänglich, sondern gestattet auch die Unterscheidung unterschiedlicher Komponenten anhand ihrer spektroskopischen Eigenschaften. Noch leistungsfähiger sind Multiwellenlängen-Detektoren, die ganze Spektren registrieren.
4. Mittels AUZ zugängliche Eigenschaften
In der Analytischen Ultrazentrifuge finden zwei Transportprozesse statt: Sedimentation und Diffusion. Die Sedimentation wird durch die Partikeldichte und die Partikelreibung bestimmt. Die Diffusion hingegen ist von der Partikeldichte unabhängig. Die relevanten Partikeleigenschaften sind also die Dichte, das Reibungskoeffizientenverhältnis und die Masse.
Alle Prozesse in der Analytischen Ultrazentrifuge beschreibt die bereits seit 1929 bekannte Lammsche Differentialgleichung:
\frac{\partial}{\partial r} \left[ r \cdot D \, \frac{\partial
c}{\partial r} – s \, \omega^2 \, r^2 \, c \right]\)
Diese ist nicht geschlossen lösbar, stellt jedoch die Basis für alle weiteren Auswertungsverfahren dar. In ihr sind die oben erwähnten Transportgrößen in Form der Sedimentationskonstanten \(s\) und der Diffusionskonstanten \(D\) enthalten. \(r\) ist eine Ortskoordinate, die Entfernung von der Rotationsachse.
Ein Partikel im Sedimentationsfeld unterliegt drei Kräften: der Fliehkraft, dem Auftrieb und der Reibung. Während die Fliehkraft von Partikeleigenschaften unabhängig ist, wird der Auftrieb von Volumen und Dichte des Partikels bestimmt. Die Reibung wiederum hängt von Größe und Form des Partikels ab. Dieser Variablensatz beschreibt also die gerichtete Bewegung eines Partikels im Sedimentationsfeld.

Die Verknüpfung der Transportgrößen \(s\) und \(D\) mit den Partikeleigenschaften Masse und Dichte erfolgt anhand der Svedberg-Gleichung:
M = \frac{s \, R \, T}{D \left( 1 – \bar v \, \varrho \right)}\)
Dabei sind die Reibungseigenschaften des Partikels im Diffusionskoeffizienten enthalten. Die Svedberg-Gleichung stellt die Grundlage für die meisten Auswertungen von AUZ-Experimenten dar.
4.1 Die Primäraussage: Sedimentationsgeschwindigkeit
Beim Sedimentationsgeschwindigkeitsexperiment wird eine Konzentrationsverteilung innerhalb der Meßzelle registriert, die direkt und ohne weitere Annahmen in eine Sedimentationskoeffizientenverteilung (\(s\)-Verteilung) umgerechnet werden kann.
Der Sedimentationskoeffizient sagt aus, wie schnell das Partikel im Einheitsfeld um eine bestimmte Wegstrecke sedimentiert. Es handelt sich um die primäre Meßgröße; es wird nicht interpretiert, aufgrund welcher Partikeleigenschaften die Sedimentation mit dieser Geschwindigkeit erfolgt.

Die Sedimentationskoeffizientenverteilung liefert bereits eine Fülle an Informationen: so sind u. a. Anzahl und Konzentration der Komponenten, Homogenität der Probe, Aggregate und Verteilungsbreiten zugänglich. Für die Lösung eines analytischen Problems reichen diese Ergebnisse oftmals schon aus.
4.2 Teilchengrößen
Eine der wichtigsten Kenngrößen in den Kolloidwissenschaften ist die Teilchengrößenverteilung (TGV), die man direkt aus der \(s\)-Verteilung errechnen kann.

Hierzu muss die Partikeldichte bekannt sein. Ist dies nicht der Fall, so kann sie anhand der Dichtevariationsmethode mit der AUZ oder mit einer unabhängigen Methode bestimmt werden. Besonders unkompliziert ist diese Auswertung für globuläre und nicht gequollene Partikel. Ansonsten sind zusätzliche Annahmen bzw. Informationen erforderlich.
Selbst kleinste Kolloide können in Ångström-Auflösung charakterisiert werden.
4.3 Teilchendichten und -verteilungen
Auch bei uneinheitlicher Partikeldichte oder ohne Kenntnis derselben lassen sich Teilchengrößenverteilungen berechnen. Dabei wird zusätzlich eine Dichteverteilung über alle detektierten Partikel erhalten. Hierzu wird das Verfahren der Dichtevariation eingesetzt, bei dem die zu untersuchenden Partikel in zwei Lösemitteln unterschiedlicher Dichte sedimentieren.
Das Verfahren existiert sowohl für Sedimentationsgleichgewichtsexperimente als auch für Sedimentationsgeschwindigkeitsexperimente. Im ersten Fall werden Gewichtsmittel für die Dichte und die Molmasse erhalten, das zweite Experiment ermöglicht das simultane Bestimmen einer Teilchendichte- und einer Teilchengrößenverteilung.

4.4 Molmassen und Molmassenverteilungen
Die Bestimmung von Molmassen ist eine klassische Anwendung der AUZ. Hierzu existieren zwei Varianten: das Sedimentationsgleichgewicht liefert gewichtsgemittelte Molmassen, die Sedimentationsgeschwindigkeit ergibt Molmassenverteilungen.

Das Sedimentationsgleichgewicht stellt sich ein, wenn die Rückdiffusion vom Zellboden und die Sedimentation zum Zellboden hin sich in einem stationären Zustand ausgleichen. Dann finden keine Transportprozesse mehr statt, und die Molmasse wird unabhängig von Sedimentations- und Diffusionskonstante erhalten.
Daher ist diese Bestimmungsmethode sehr genau, der Fehler liegt unter 3%. Allerdings kann diese Genauigkeit häufig auch mit Sedimentationsgeschwindigkeitsexperimenten erreicht werden. Das Gleichgewicht ist besonders für sehr kleine Teilchen geeignet, die rasch diffundieren, so dass sich das Gleichgewicht schnell einstellt.
Da sich im Gleichgewichtsprofil mehrere Spezies überlagern können, sind zur Anpassung meist Annahmen erforderlich, z. B. hinsichtlich der Anzahl und relativen Konzentration der Spezies.
Wir verwenden daher zur Auswertung vorzugsweise die modellunabhängige \(M\)*-Funktion, aus der geeignete Modelle abgeleitet werden können, ohne dass zu unsichere Annahmen über die Natur des Systems zur Auswertung erforderlich sind.
Im Sedimentationsgleichgewicht müssen stets Konzentrationsreihen untersucht werden. Dabei wird auch der Zweite Osmotische Virialkoeffizient erhalten.

Aus dem Sedimentationsgeschwindigkeitsexperiment werden ganze Molmassenverteilungen erhalten. Dazu muss jedoch für jede Spezies deren Dichte und Reibungskoeffizientenverhältnis bekannt sein.
4.5 Teilchenform und Teilchenquellung
Die Sedimentationsgeschwindigkeit eines Teilchens bietet einen Zugang zu dessen Reibungseigenschaften, die durch das Reibungskoeffizientenverhältnis \(f/f_0\) beschrieben werden. Aus Meßgrößen der AUZ berechnet sich dieses nach
\frac{f}{f_0} = \frac{M \left( 1 – \bar v \varrho_0 \right)}{N_A \cdot 6 \pi \eta_0 s^2_{20, w}}
\cdot \sqrt[3]{\frac{4 \pi N_A}{3 \bar v M}}.\)
Für eine kompakte Kugel ist \(f/f_0\) Eins; für nichtglobuläre Partikel kann anhand des Reibungskoeffizientenverhältnisses das Achsenverhältnis eines Ellipsoides berechnet werden, wenn die Molmasse bekannt ist. So kann ein derartiges Partikel durch Kombination von Sedimentationsgeschwindigkeit und -gleichgewicht charakterisiert werden.
Auch für gequollene Partikel ist \(f/f_0\) größer als Eins, so dass auf diese Weise der Hydratationsgrad berechnet werden kann. Je komplexer das Partikel, um so größer ist der Bedarf an Informationen zu einer vollständigen Charakterisierung. Die verschiedenen Meßtechniken der AUZ und die Kombination mit anderen Methoden bieten zahlreiche Optionen, einen vollständigen Variablensatz zu erhalten und auch komplexe Partikel umfassend zu beschreiben.
4.6 Wechselwirkungen
Interpartikuläre Wechselwirkungen äußern sich in der AUZ
- in der Konzentrationsabhängigkeit des Sedimentationskoeffizienten (\(k_s\), Sedimentationsgeschwindigkeit),
- in der Konzentrationsabhängigkeit der apparenten Molmasse (\(A_2\), Sedimentationsgleichgewicht).
Durch Aufnehmen von Konzentrationsreihen werden wertvolle Informationen über die Wechselwirkungen gewonnen. Die erhaltenen Parameter lassen sich auch mit einschlägigen Parametern anderer Methoden kombinieren.
Auch Dissoziationskonstanten aggregierender Systeme sind auf diese Weise zugänglich.
4.7 Diffusion
Wie die Lammsche Differentialgleichung zeigt, treten die Transportprozesse der Sedimentation und der Diffusion immer gekoppelt auf. In der Vergangenheit wurde die Diffusion als störendes Phänomen wahrgenommen, da sie zu einer Verbreiterung der gemessenen Verteilungen führt. Ihr Einfluss wurde durch geeignete Wahl der Versuchsbedingungen und durch spezielle Auswertungsverfahren unterdrückt; diese Arbeitsweise erweist sich auch heute noch oft als sinnvoll.
Andererseits unterliegen die beiden Prozesse unterschiedlichen Zeitgesetzen und können so prinzipiell separiert werden. Mit modernen Rechnern und Algorithmen ist es möglich geworden, globale Datenanpassungen vorzunehmen, welche die Diffusions- und Sedimentationsprozesse gleichzeitig beschreiben – so ist die ”störende“ Diffusion zu einer Quelle von Information geworden.
Wenn auch Diffusionskoeffizienten anhand der Dynamischen Lichtstreuung mit geringerem Aufwand bestimmt werden können, gibt es Fälle, bei denen die AUZ auch heute noch zur Messung von \(D\) herangezogen wird.
4.8 … und vieles mehr
Der versatile Einsatz der AUZ bedingt, dass weit mehr Fragestellungen bearbeitet werden können als die zuvor genannten. So lässt sich die AUZ als Druckgenerator nutzen, um Emulsionen unter hohen Drücken zu entmischen und damit Stabilitäten wesentlich schneller zu bestimmen als nach herkömmlichen Verfahren. Ebenso kann die Entquellung von Gelen erzwungen und thermodynamisch ausgewertet werden.
Auch die optischen Systeme der AUZ können sehr variabel eingesetzt werden. So können verschiedene Spezies mit unterschiedlichem Absorptions- oder Refraktionsverhalten in ein und demselben Experiment getrennt registriert werden. Die spektralen Eigenschaften der verschiedenen Komponenten bieten sogar einen orthogonalen Zugang zur Analyse des Systems (”Multiplex- Analyse“ ).
Der Fantasie und Kreativität des Experimentators bietet die AUZ viel Raum. Zugänglich sind nicht nur eine Vielzahl dispergierter Systeme, sondern auch komplexe Objekte: beladene und unbeladene Kapside, selbstorganisierende Überstrukturen, core-shell-Partikel und vieles mehr.

5. Kombination mit anderen Methoden
Als hydrodynamische Absolutmethode lässt sich die AUZ hervorragend mit anderen Methoden kombinieren. Da ihre Meßergebnisse von keiner Kalibrierung abhängig sind, sondern aus fundamentalen hydrodynamischen Gesetzmäßigkeiten gewonnen werden (”ab initio“), können die Ergebnisse mit solchen aus anderen Methoden abgeglichen oder verknüpft werden.
Dies gilt um so mehr, als die AUZ einen besonders umfangreichen hydrodynamischen Parametersatz adressiert. Von diesem sind die Wechselwirkungsparameter \(k_s\) und \(A_2\) von besonderer Bedeutung, wenn sie zu Parametern anderer Methoden in Beziehung gesetzt werden, welche dort die Wechselwirkungen beschreiben. Tatsächlich ist der Wechselwirkungsparameter \(A_2\), welcher aus einer Reihe von Sedimentationsgleichgewichten gewonnen wird, identisch mit eben jenem Zweiten Osmotischen Virialkoeffizienten \(A_2\) aus der Statischen Lichtstreuung.
Besonders ergiebig ist die Kombination mit der Viskosimetrie. So können anhand hydrodynamischer Formfunktionen die Achsenverhältnisse nichtglobulärer Partikel bestimmt werden. Als Beispiele seien die Funktionen \(ν\), \(P\) und \(R\) genannt:
\nu = \frac{[\eta]}{v_s}\)
P = \frac{M \left( 1 – \bar v \varrho_0 \right)}{N_A \cdot 6 \pi \eta_0 s^0_{20, w}}
\cdot \sqrt[3]{\frac{4 \pi N_A}{3 \bar v M}} \cdot \sqrt[3]{\frac{1}{\frac{w}{\bar v \varrho} + 1}}\)
R = \frac{k_s}{[\eta]} \approx \frac{2 \left( 1 + P^3
\right)}{\nu},\)
Diese Funktionen nehmen für bestimmte Achsenverhältnisse definierte Werte an. Der verwendete Variablensatz ist vollständig aus der AUZ zugänglich, außerdem wird die intrinsische Viskosität \([\eta]\) aus der Viskosimetrie verwendet. Weiterhin tritt das mittlere partielle spezifische Volumen eines gequollenen Partikels \(v_s\) bzw. die Hydratisierung \(w\) auf. Für ein nicht gequollenes Partikel ist dieser Parameter gleich \(\bar v\), dem partiellen spezifischen Volumen. Für gequollene Partikel kann dieser Parameter eingesetzt werden, oder man verwendet hydratisierungsunabhängige Funktionen wie die Berechnung der Molmasse nach Lavrenko oder die \(\Pi\)-Funktion:
M = N_A \cdot \sqrt{\left( \frac{6 \pi \eta s}{1 – \bar v \varrho} \right)^3}
\cdot \sqrt{ \frac{3 k‘ [\eta] \bar v}{4 \pi k_s} \left(\frac{k_s}{2 \bar v} – \frac{k‘ [\eta]}{k_s} \right)
};\)
\frac{v_s}{\bar v} = \frac{k‘ [\eta]}{k_s},\)
\Pi \approx \frac{2 A_2 M}{[\eta]},\)
die andere Parameter verwenden, um den Variablensatz zu vervollständigen.
Bei aller Kompatibilität mit anderen Methoden besitzt die AUZ jedoch auch ein einzigartiges Alleinstellungsmerkmal: Sie ist die einzige Methode, die anhand einer Gewichtskraft fraktioniert, und sie ist die einzige Methode, mit der Dichteverteilungen gemessen werden können.
6. Historische Methode, moderne Trends
Die AUZ leistet seit 100 Jahren ihre Dienste in der Biochemie und den Kolloidwissenschaften. Dies ist verblüffend für eine moderne physikalische Methode. Dennoch erschließt sie sich fortwährend technologisch und methodisch neue Potentiale.
Schon 1924 stellte Thé Svedberg, der Erfinder der AUZ, fest, dass ”Hämoglobin in Lösung höchstwahrscheinlich eine Molekularmasse von 66800 aufweist – in vier Untereinheiten von 16700.“ Ein früher und spektakulärer Erfolg der Analytischen Ultrazentrifugation.

Seither ist die AUZ in Jahrzehnten der Anwendung bei der Entschlüsselung unzähliger Fragestellungen zum Einsatz gekommen. Darunter solche, die letztlich zu Nobelpreisen führten – wie die Strukturaufklärung der DNS. In den vergangenen Jahrzehnten hat sie zudem mit der enormen Entwicklung der Kolloidwissenschaften in ihrem ursprünglichen Einsatzgebiet neue Anwendungen gefunden.
Zudem profitiert die AUZ vom allgemeinen technologischen Fortschritt auf dem Gebiet der Photonik und Elektronik. Nach jahrzehntelangem Stillstand seit Einführung der Absorptions- und Interferenzoptik wurden seit 2010 mehrere moderne Detektoren entwickelt – vor allem die Multiwellenlängenabsorptions– und -emissionsdetektoren bergen das enorme Potential, den Meßergebnissen eine spektrale Dimension hinzuzufügen. Darüber hinaus wurden Fluoreszenz- und Interferenzdetektoren verbessert, und weitere Detektoren (Raman, Trübung, Streuung) befinden sich in der Entwicklung oder existieren bereits als Prototypen.

Der größte Fortschritt liegt jedoch darin, dass es mit modernen Computern und Algorithmen möglich geworden ist, globale Datenanpassungen an die Gesamtheit der Meßdaten vorzunehmen. Diese Entwicklung hat die AUZ revolutioniert – und birgt noch großes Potential.
7. AUZ als Auftragsmessung
Eine Analytische Ultrazentrifuge ist teuer. Zudem erfordert ihr Betrieb Expertise und Erfahrung. Daher ist es attraktiv, diese Methode in Form von Auftragsmessungen zu betreiben.
Nanolytics war das erste Auftragslabor mit Schwerpunkt Analytische Ultrazentrifugation in Europa. Seit über 20 Jahren bietet Nanolytics nicht nur Messungen auf hochwertigen Geräten an, sondern umfangreiche Expertise im experimentellen Design und der gründlichen Auswertung der Meßergebnisse.
Nanolytics verfügt über die fortgeschrittensten Detektoren, u.a. der Multiwellenlängen-Absorptionsdetektion und dem Aida-Detektor (Advanced Interference Detection Array) von Nanolytics Instruments. Damit sind Messungen in sehr viel verdünnteren und konzentrierteren Systemen möglich als mit marktüblichen Detektoren.
Diese hochwertige und einzigartige Ausstattung in Verbindung mit einem hochspezialisierten und erfahrenen Team bietet die Gewähr für beste Ergebnisse – ob für Routinefragestellungen oder bei der Charakterisierung komplexer Systeme.

